ASCON轻量级密码原语：资源受限环境中能够高效运行的基本密码学算法和操作。

⊕：按位异或运算，对二进制数对应进行操作，相同为零，不同为一，如101⊕110=011 ≫：循坏右移，将二进制数向右移指定位数。 计算过程：将x0循环向右移19位得到一个新的64位二进制数，再将x0循环向右移28位得到一个新的64位二进制数，然后将三部分的二进制数进行异或运算，最后得到的数赋值给新的x0。其他步骤也是类似的。

汉明权重：汉明权重是指二进制向量中非零元素的个数，如11001100，汉明权重的个数为4。

量子门：受控非门（CNOT)和交换门(SWAP)

CNOT(受控非门）：图中a上方部分表示目标比特a，下方表示控制比特b,小圆点表示控制位标识

操作逻辑：当控制比特a=1时，目标比特与1进行异或操作，当a=0时，目标比特保持不变。输出a ⊕b和b。如，当控制比特a为1，目标比特b为0时，按照原理，目标比特首先和1进行异或运算得到1，然后进行控制比特a=1和目标比特b=0进行异或运算得到1，因此最终结果得到，a⊕b=1,目标比特b=1。当控制比特a=0,目标比特b=1时，按照原理目标比特b不需要改变，然后进行异或运算a⊕b=1,最终结果得到a⊕b=1,b=1。

SWAP（交换门）：图b中，两条线分别表示两个量子比特a,b，交叉线和x两个标识表示交换操作。操作逻辑：作用交换两个量子比特的状态，输入a和b，输出b和a,若两个两字比特不相邻则无法直接进行交换。

区分CNOT门和SWAP门方法：CNOT的符号通常用⊕来表示，如果某两条线间出现了⊕则表示存在CNOT门，而SWAP门的符号为x来表示，如果某两条量子比特线间出现了X则表示存在SWAP门。

分为三个过程：第一部分为受控非门：出现了两个CNOT门（控制比特x3和目标比特x1，控制比特x1和目标比特x2）这两个操作可以看作为同时进行的。第二部分SWAP门操作：作用于x2,x3，这是在第一部分的基础上进行交换的。第三部分CNOT操作:同样出现了两个CNOT门（控制比特x3和目标比特x2，控制比特x1和目标比特x3）这两个操作可以同时进行。例如假设x0=0，x1=0，x2=0，x3=1。第一次CNOT的操作为控制比特x1=0，目标比特x2=0，则进行操作后得到x1=0，x2=0第二个CNOT的操作为控制比特x3=1，目标比特x1=0，进行操作后得到x3=1，x1=1

最终结果为x0=0，x1=1，x2=0，x3=1

第二部分进行SWAP门：基于第一部分的操作X2和x3进行交换，得到x0=0，x1=1，x2=1，x3=0

第三部分CNOT:基于第二部分进行操作，也分为两部分，第一次控制比特x1=1，目标比特x3=0，进行异或操作得到x1=1,x3=1,第二次控制比特x2=1，目标比特x1=1进行操作得到x0=0,x1=0,x2=1,x3=1。

引入辅助变量全是零的优点：零与任意比特变量进行异或都得到该变量的本身。辅助变量可以储存原始量子比特的副本，为后续可能的量子算法操作提供额外的量子比特资源。

如图例2中第三行与单位矩阵的第三行相同，所以不需要将该行复制给辅助变量。

例3中第0列和第2列与单位矩阵的第0列和第2列相同，所以也不用复制给辅助变量。

辅助量子比特重置为零需要借助CNOT操作来实现，因此会增加CNOT门数量所以得到总结：

1.并非所有原始量子位都得到更新（当矩阵的第i行与单位矩阵的第i行完全相同时会发生这种情况）。

2.并非所有原始量子位都需要用于更新其他量子位（当矩阵的第i列与单位矩阵的第i列完全相同时会发生这种情况）。

高斯-约旦消元法：通过对初等矩阵进行一系列的初等行变化，将其化为最简初等矩阵，从而直接得出线性方程组的解。

如图中的矩阵来分析：我们目的是将矩阵化为最简初等矩阵，观察可知第二行和第三行可进行变化，将第二行和第三行进行异或操作得到：即（x2 ← x2 ⊕ x3）

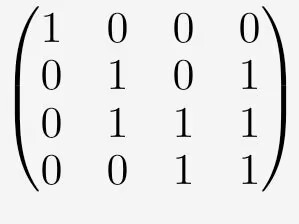
构建对应的初等矩阵，对单位矩阵进行对应的异或操作，得到第一初等矩阵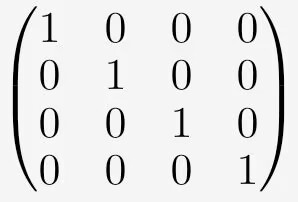

进行（x2 ← x2 ⊕ x3），得到：

在第一的初等矩阵变化下进行第二次变化观察得到第二行和第三行可进行交换得到矩阵

构建初等矩阵，对单位矩阵进行同样的交换得到：

第三步在第二步的基础上继续进行变化，观察得到第一行和第三行进行变化，即进行（x1 ← x1 ⊕ x3）得到矩阵：

进行初等构建得到：

同样将第二行和第三行进行异或操作，赋值给第二行：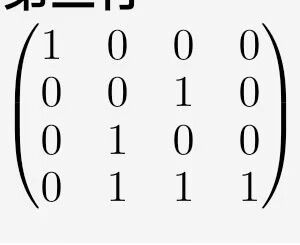

构建初等矩阵：

将第一行和第三行进行异或赋值給第四行得到：

构建初等矩阵：

第一行和第二行进行交换得到矩阵：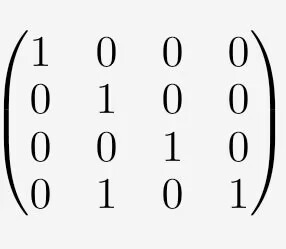

构建初等矩阵得到：

最后一步将第一行和第三行进行异或赋值给第四行，得到：

构建初等矩阵得到：

最后得到原矩阵为：=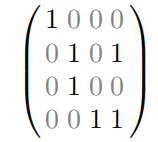

PLU分解法：

置换矩阵：具有每行每列只有一个非零元素（值为1）的特点，它的作用是对矩阵的行进行置换。

下三角矩阵：主对角线以上元素全为0的矩阵。

上三角矩阵：主对角线以下元素全为0的矩阵。

ASCON作为轻量级加密原语，保障数据的传输安全。而量子计算的崛起为优化密码算法性能带来了新的机遇。

这篇论文中，主要是将ASCON线形层转化为320x320的二进制矩阵。而为了实现原位计算可以采用多种方法，比如高斯约旦消元法，PLU分解法等。而在此基础上还对XZBLZ进行了改进，改进后XZBLZ算法能够计算处理更大的矩阵，还能灵活选择是否进行最终标记。

从性能来看，朴素实现，高斯约旦消元法，PLU分解法和改进XZBLZ算法在量子比特数，CNOT门数和量子深度等指标上的差异。结果显示，改进XZBLZ算法十分出色，大大优化了量子资源的利用。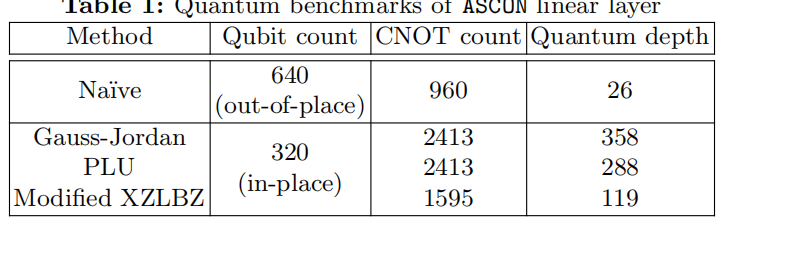

这次项目首次完成了ASCON线形层的原位量子实现，并给出了4种实现方式。其中改进后的XZBLZ算法优势明显。而这篇论文主要介绍了高斯约旦消元法和PLU分解法的详细过程。高斯约旦消元法和PLU分解法都是通过对行对列来实现的，不同的是高斯约旦消元法是通过对行对列进行变化，最终得到一个单位矩阵，而PLU分解法则是通过对行对列的变化得到置换矩阵，上三角矩阵，下三角矩阵。而高斯约旦消元法通用但深度大，PLU分解法结构化分解，平衡性较好，而高斯约旦消元法和PLU分解法对XZBLZ起到了辅助作用，在两种传统的帮助下矩阵可以化简为多个小矩阵，使得效率更高。